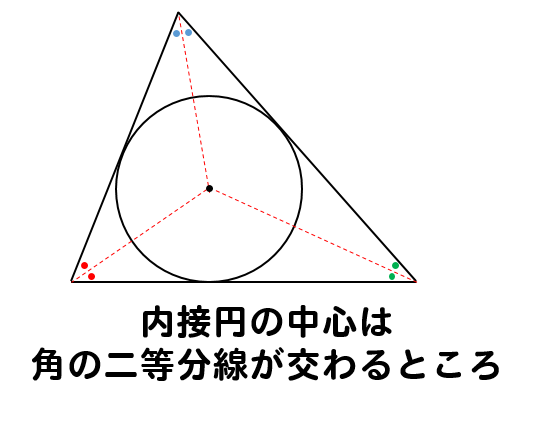
三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。A 級2 分30 秒;・「三角形の内角」180°から見て c = 180°(ab) ① ・「直線」(Bl) 180°から見て c = 180° g ② ①=②(c = c)より 180°(ab) = 180° g ab = g g = ab // 「三角形の内角の和」も「直線」も、「どちらも」180°ということを、
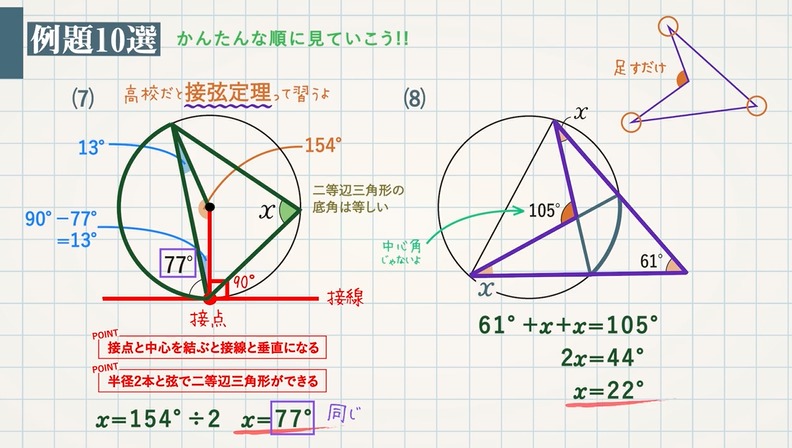
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
円 内接 三角形 角度
円 内接 三角形 角度-つまり、円に内接する三角形で1°をはさむ2辺の長さが (m,k) のとき、反対側に頂角が60°の三角形を張り合わせて内接四角形を作るとき、その辺の長さの組み合わせ(もちろん無数にあるが)のうち、等脚台形になる (m+k,k) の場合と、(m,m+k) の場合については、七五三三角形同様マークなら暗算で処理してしまいたくなる。B 級3 分 秒;



1
三角形は二等辺三角形と呼ばれ、2辺が等しいことに注意してください。 この三角形の底辺の角度も等しくなるはずです。 そのような三角形は、同時に、円に内接し、その周りに記述することができます。 2 まず、三角形の未知の底辺を見つけます。この円は bed の外接円,すなわち円o である。したがって,四角形abcd は円o に内接する。 イント 弧に対する中心角は1つに定まることを用いる。 イント 一直線上にない3点を通る円はただ1つに定まることを用いる。 三角形の内接円、外接円、面積、角度 外接円の中心と半径を求めるコードを作ってみました。 公式がわからなかったので、 Wikipedia の外接円の項目を参照しました。 (x1)^2 (y2)^2=3^2という円の方程式の形で結果を出力します。 小数の場合は小数点以下2桁までに四捨五入し、必要のなくなったゼロは消去。 うまく丸める処理が思いつきませんでした。 その後に
数学の問題です。 半径aの円に内接する三角形があります。 この三角形の各辺の中点を通る円があります。 この円の面積をaを使って表して下さい。 / 三角形の相似を使う問題ですね。 最初の円の面積の1/4になるでしょう。 これは中学生の宿題ではないのですか?点Dを中心に円を書くと j Dを中心に三角形の3つの辺に接する 円を書くことができます。 この円を 内接円といい、中心を内心といいます。 下の「定理8」は三角形の3つの角の二等分線は1点で交わること の証明ですが、その証明方法をはじめてみる方にとっては、「へぇ~ 垂線か」と思われるかもしれませんが、「角の二等分線」が「各辺から の距離が等しい②接点三角形←→接線三角形 (内接円の) ③垂足三角形←→傍心三角形 (角度)・・・これが意外でした。 ④チェバ三角形←→逆チェバ三角形 (楕円の) s:これらはみな同じ「三角形からできる三角形」の構造ということですね。
三角形には不思議な性質がたくさんあります。 その中にはまだ発見されていないものもあるはずです。 このジオジェブラを使うと正確な作図が簡単にでき、さらにアニメーションを使って変化を調べることができ、新しい発見が容易にできます。 「bもしかしたら・・・?前回 https//googl/EVb9HF 次回 https//googl/jPrhyo動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が4 分 秒) (1) {\iac = 35 \iba = 22 a b c i (2) {\ibc = 40 \aib = 117 a b c i (3) \bac = 72 a b c i (4) \bic = 140 a b c i



円と三角形 角度 中学から数学だいすき



数学a 接弦定理の使い方とコツ 教科書より詳しい高校数学
円に内接する三角形の面積 中学入試問題に悩んでいます。 考えても見当がつきませんでしたので、どなたか、ご回答をお願いいたします。 半径5の円に内接する ABCがある。 AB=8,AC=2√10とし、点Aから辺BCに垂線ADを引いてできる ADCの面積を求めよ。 図が右図において,緑で示した2つの角は,一つの弧 に対する円周角だから等しい. ∠ ABE=60° また, ∠ AEB は ∠ BEC の補角だから ∠ AEB=180°−110°=70° 次に,三角形の内角の和は180°だから円に内接する三角形の角度xを求める問題がどうしてもわかり ∠abc=90° (aocは直径だから) ∠ocb=∠obc=18° (⊿obcは2等辺三角形だから) x= ∠oba=∠abc∠obc=90°18°=72° こんにちは。



円に内接する三角形の角度xを求める問題がどうしてもわかりません Yahoo 知恵袋




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
円の中心を内側に含む内接三角形を考える。 中心から底辺までの長さをx(0=<x<r)として、高さはx+rで表される。 さらに、中心から底辺の一端に補助線を引くと高さx、斜辺rの直角三角形ができる。 三平方からこの三角形の底辺は√(r^2x^2)であり、これを2反射テスト 角度 三角形と内接円 01 1 abc の内心をi とする わかる角度全てを図に書きこめ(s 級1 分50 秒;接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわって、 a+b+c=90° b+cーa=90° 外心の角度の関係 その2



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ
ビデオ 高校 数学Ⅰ 三角比33 内接円の半径 (14分) 21, 七月 すべての辺の長さが同じ 平行四辺形 は ひし形 と呼ばれます。 この基本的な性質は、そのような平らな幾何学図形の反対側の頂点にある角度の等価性を決定します。三角形と内接円の接線01 小6以上。三角形とその内接円があるとき、線分の長さを求める問題です。解説を読むのに中学生以上の知識が必要ですが、小学生でもできないことはないでしょう。 比 倍率と長さ01 比から、倍率を考えて長さを求める問題です三角形の辺の比 三角形の五心 チェバの定理、メネラウスの定理 円に内接する 四角形 円と直線 方べきの定理 2つの円 準備中 準備中 準備中 答表示 印刷 外心、内心の基本問題(角度) abcの外心をoとする。



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




円に関する性質その1 接弦定理 高校数学の知識庫
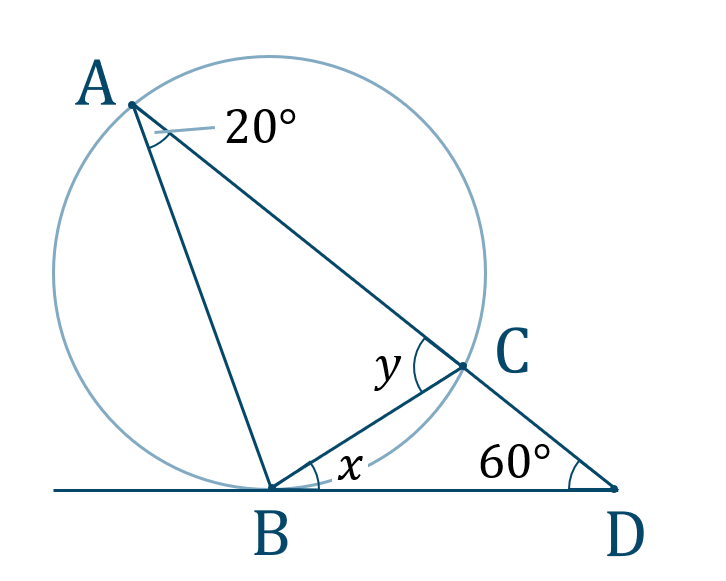
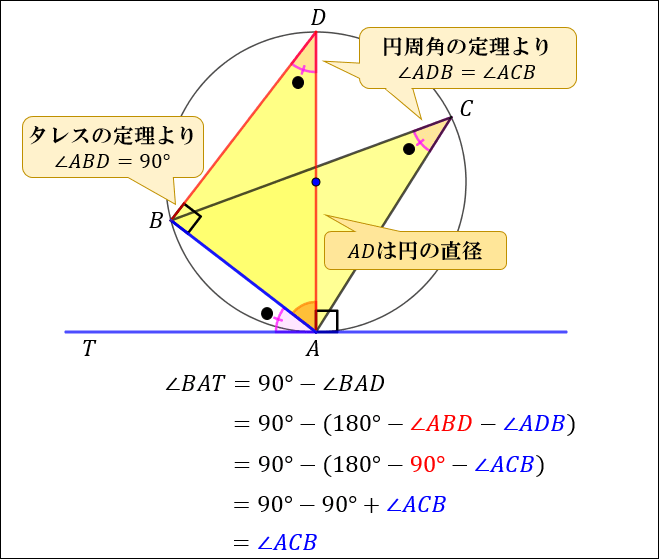
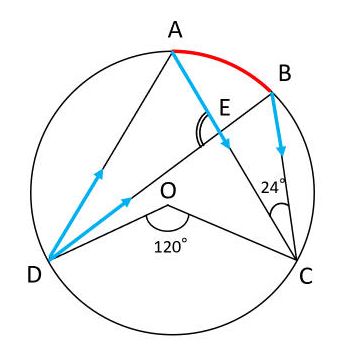
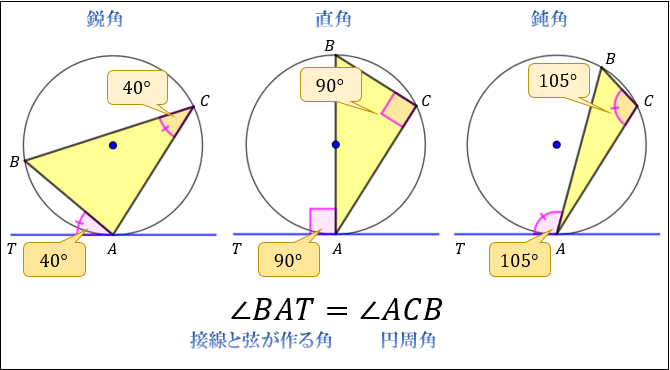
右側の三角形で内角の和は180°だから残り1つの角は70° 次に∠cと70°は円に内接する四角形の向かい合う内角だから∠c70°=180° → ∠c=110° 性質 任意の円は、任意の三つの角度を持つ三角形(もちろん角度の和は 180° に等しい)を内接三角形として持つ。 任意の三角形は適当な円に内接する(そのような円は、その三角形の外接円と呼ばれる)。 接弦定理とは? 接弦定理とは、円に三角形が内接し、その頂点のどれか \(\bf{1}\) 点を通る円の接線があるときに、それらの 角度に関して成り立つ定理 です。




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



単位円上にある異なる3点がつくる三角形の面積の最大値をどう求めますか Quora
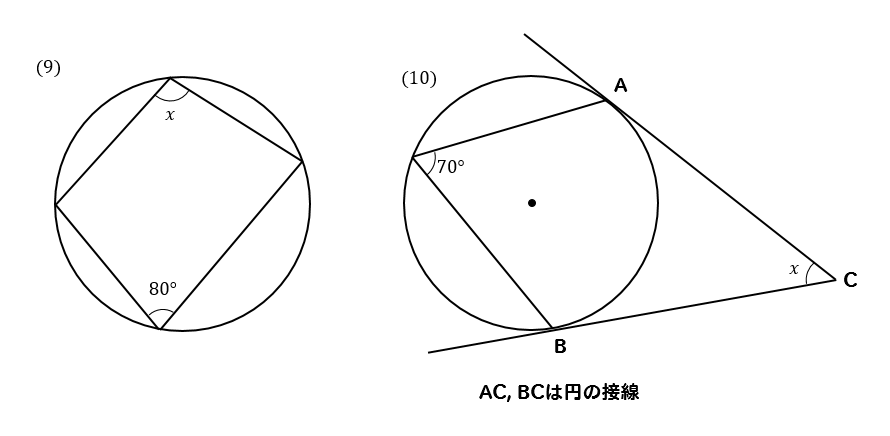
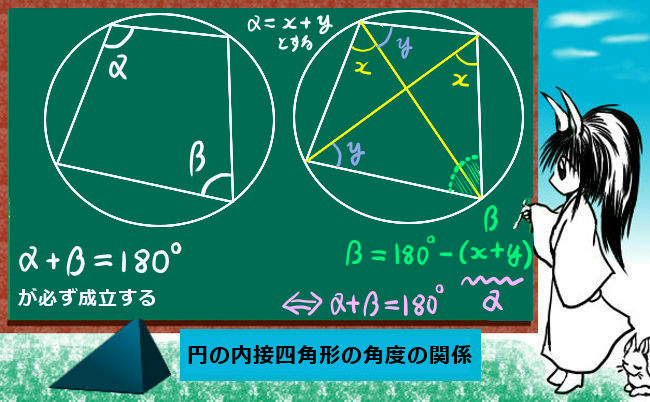
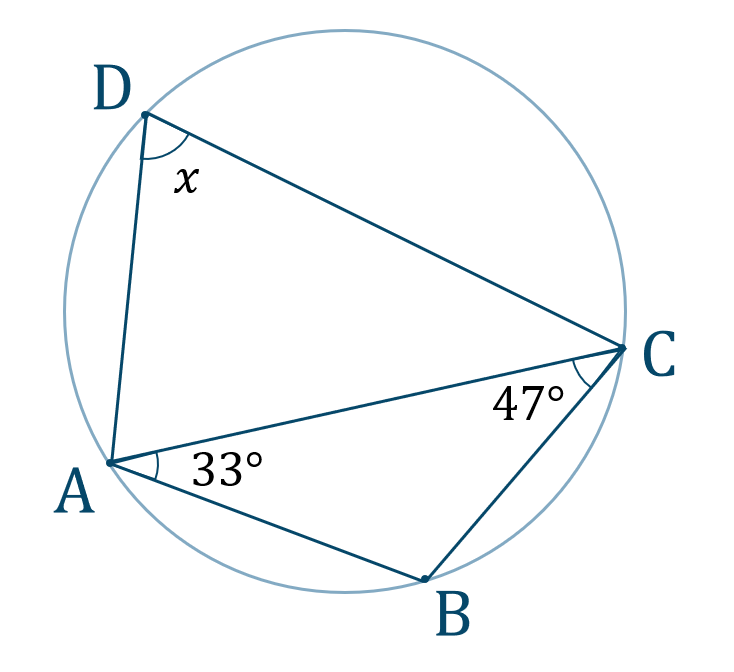
性質1の逆も成立します。つまり, 向かい合う内角の和が 18 0 ∘ 180^{\circ} 18 0 ∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABCここでは、同じ弦をもつ三角形に外接している円の特徴について説明しましょう。 図のように円の中に ABP、 AQB、 ABRがあるとします。 この三角形はABを共通の底辺としてもっていますね。 このような状況にあるとき、∠APB=∠AQR=∠ARBの大きさは同じになります。 問題をみてみましょう。 図のように、四角形ABCDがあります。 ∠BAC=30°、∠BCD=1°がわかって




円に内接する正三角形の問題 社会人になり勉強することもなくなったのですが Okwave




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
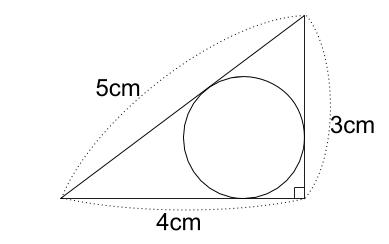
直角三角形の内接円の角度と面積 AB=4 BC=5 CA=3 の直角三角形ABCがある。 この三角形の内接円と3つの辺AB BC CA の接点をPQRとする。三角形を逆さにするとわかりやすい。 正方形に内接する円に内接する正方形は1/2。 六角形に内接する円に内接する六角形は3/4。 参考文献 『SFパズル』 マーティン・ガードナー著、上島建吉訳、紀伊国屋書店 『解ければ天才! 算数100の難問・奇問』 中村義作著、講談社 『1年遊べる奇想天外パズル』 芦ヶ原伸之著、光文社 『数学パズル』 雅孝司著、宝島社



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



円周角の定理 理数系無料オンライン学習 Kori



48s96ub7b0z5f Net Naisetsu Shikakukei



内接円 内心



三角形の内接円 中学数学の無料オンライン学習サイトchu Su
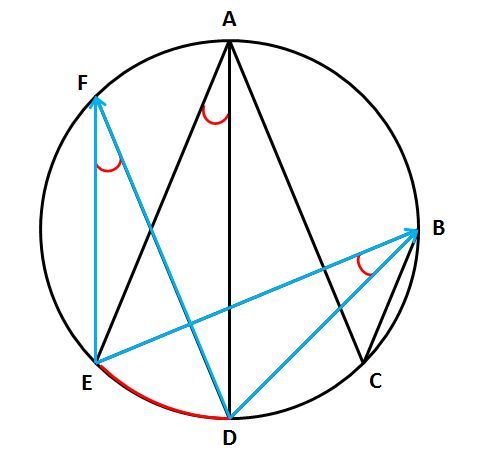



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




19 円に内接する四角形の 公式 小技 シリーズ 医学生gの数学ノート



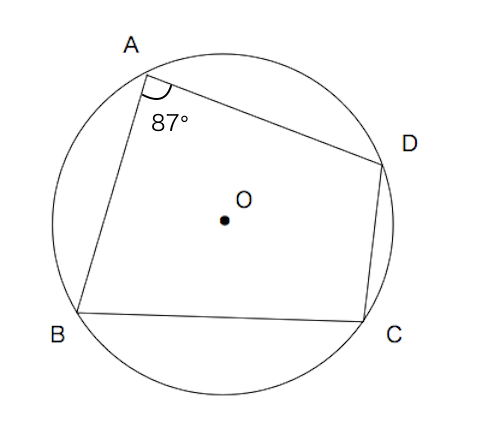
Aの角度を教えてください 円に内接する四角形の対角の和が180 よ Yahoo 知恵袋




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
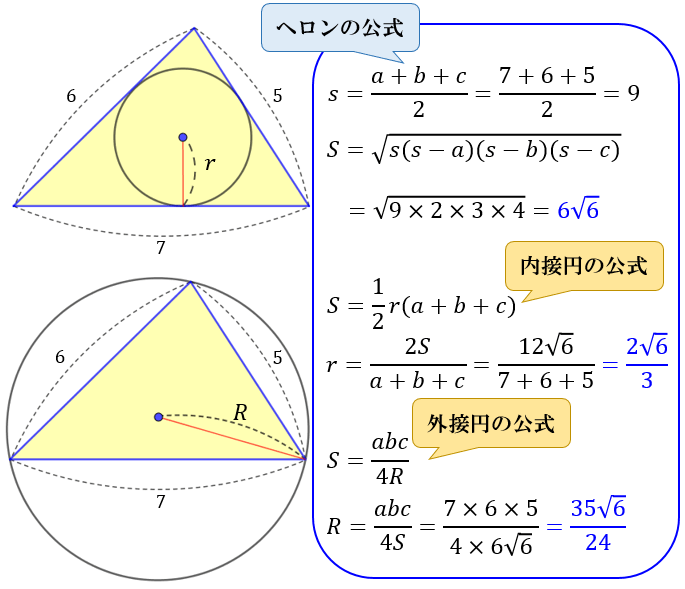



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




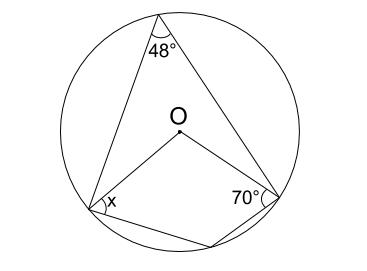
中学数学 円の中の三角形の角度の問題 お世話になります 円の中の三角形 Okwave



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に




角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ



1




接線の性質 なぜこの記号同士が同じ角度になるのかが分かりません Clear




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
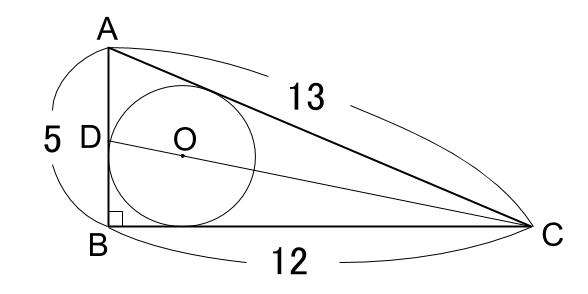



内接円と角の2等分 中学数学の無料オンライン学習サイトchu Su
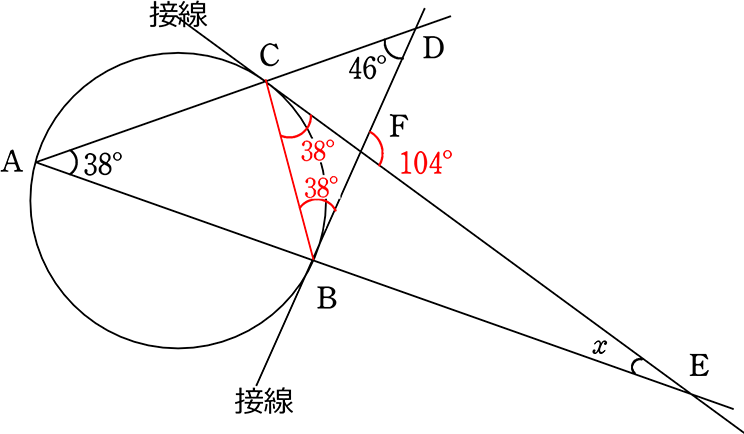



中学数学 円周角 中心角
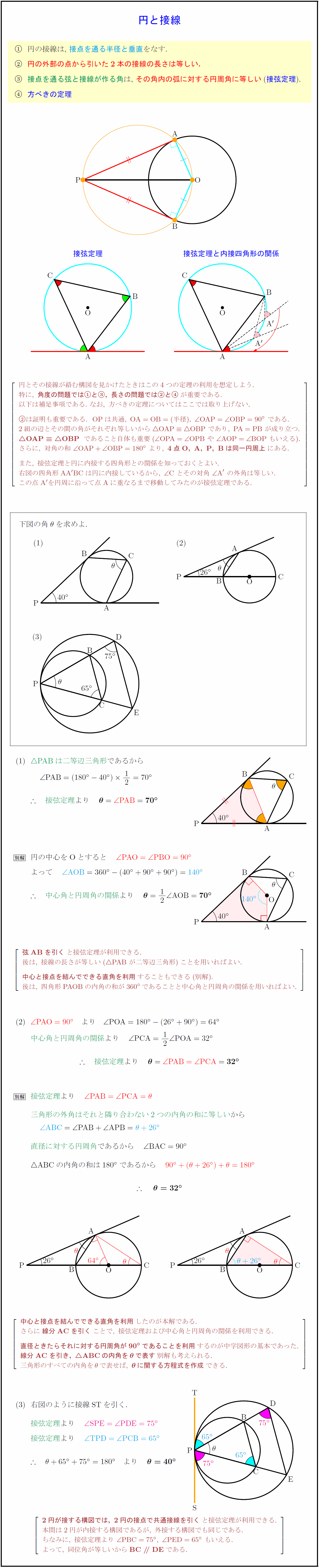



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月



数学a円に内接する四角形 xの値を求めよ 答えは50度なんですがな Yahoo 知恵袋
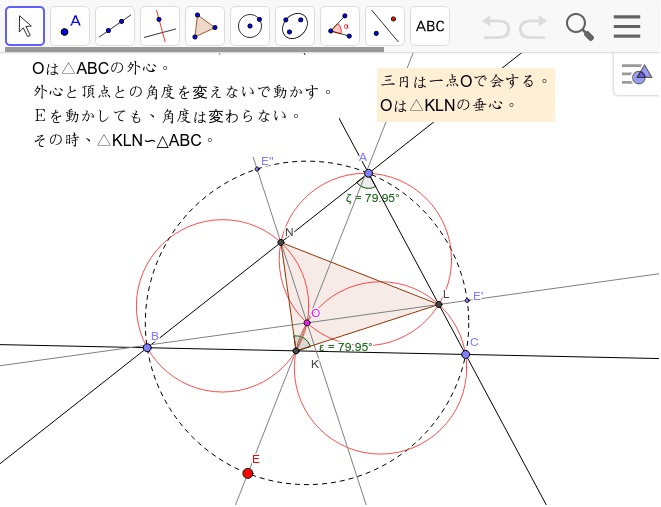



三角形に内接する相似三角形 Geogebra
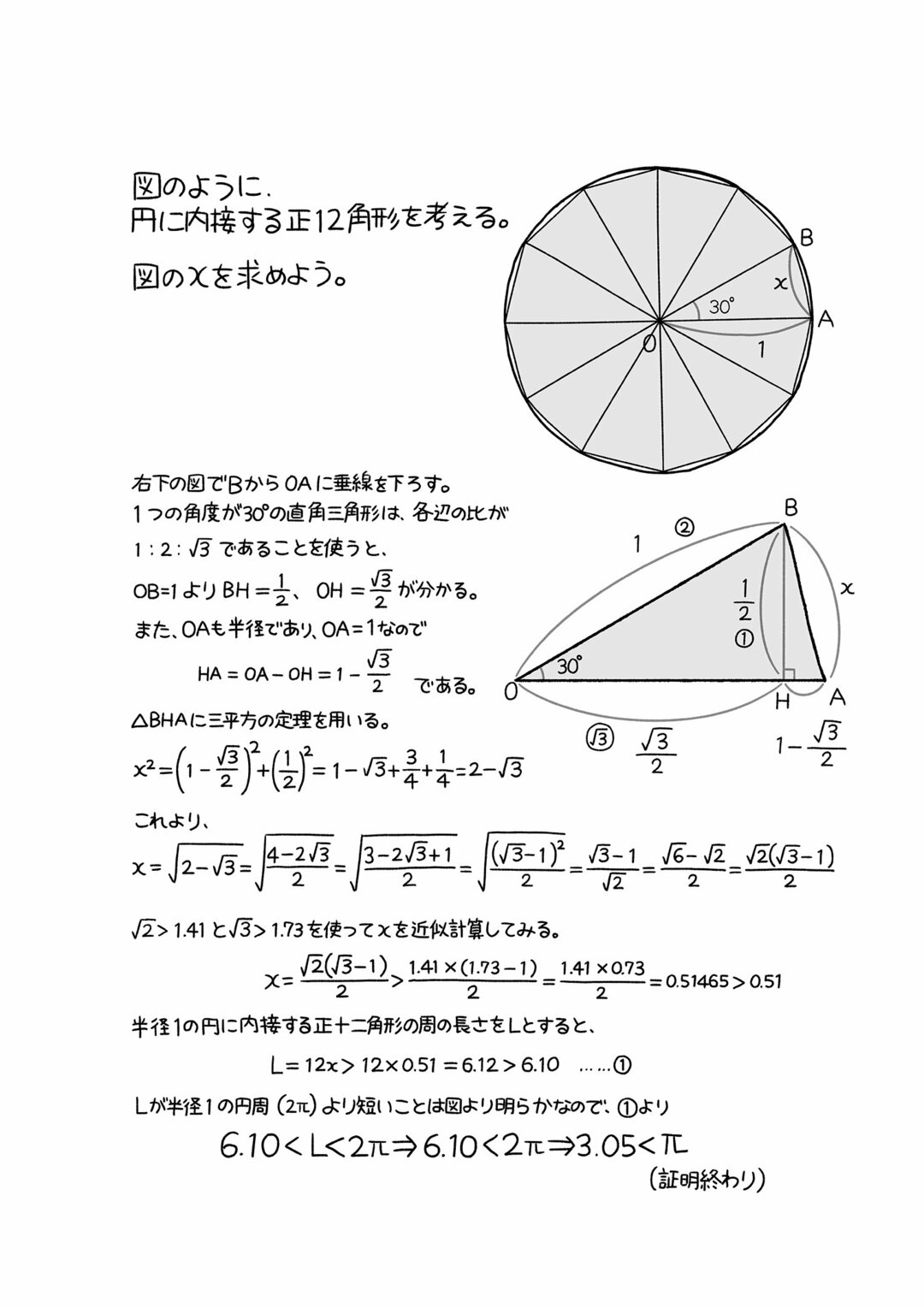



ベスト 円 内接 三角形 角度 円 内接 三角形 角度




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく



Math 円 5 直角三角形に内接する円の半径 働きアリ



内接円 内心



円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su



1



Excel Vba 数学実験室 正三角形と内接する円の面積比




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者



外接円 外心について




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




三角形の外接円の 4 つの性質 証明付 理数アラカルト



数学a 円に内接する四角形と角の使い方とコツ 教科書より詳しい高校数学
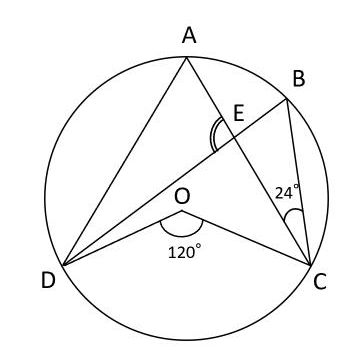



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室
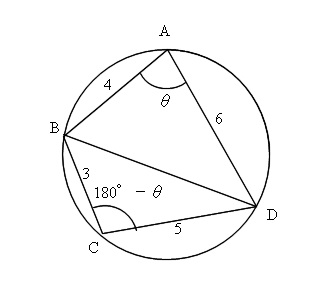



円に内接する四角形の面積の求め方と定理の使い方
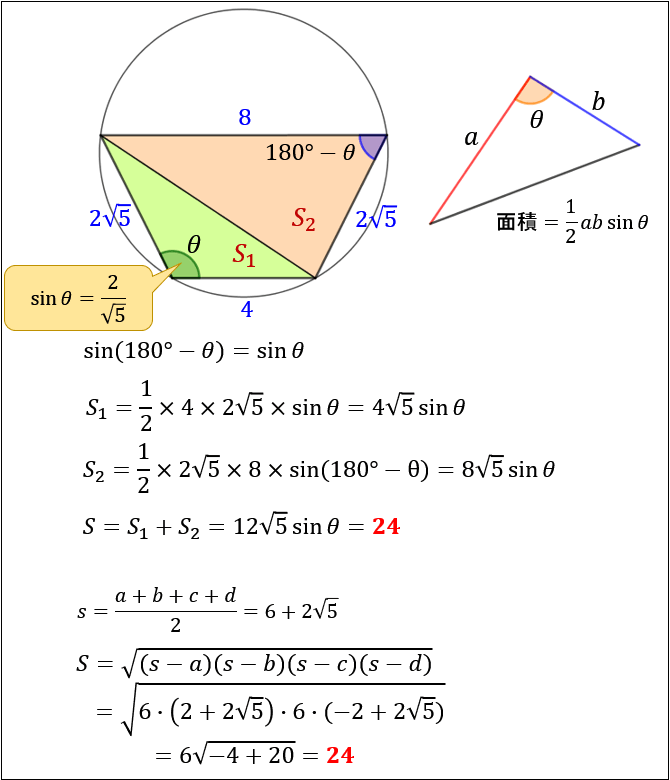



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




標準 三角比と円に内接する四角形 なかけんの数学ノート



1



Math 三角形に内接する円 働きアリ
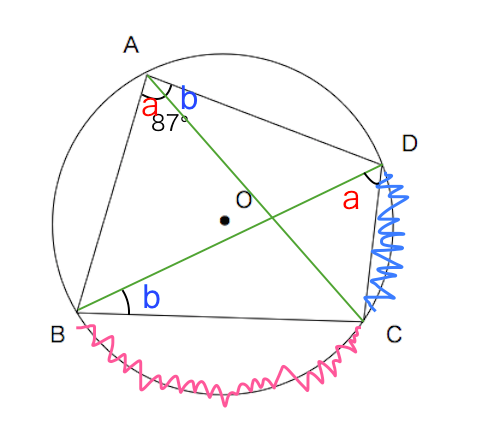



円に内接する四角形 苦手な数学を簡単に




二等辺三角形の内接円 高校入試 数学の良問を解く



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




高校数学 数 96 円に内接する四角形 Youtube
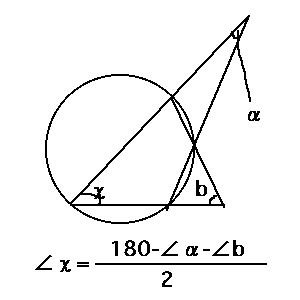



角度を求めよう 円とブーメラン 中学数学 Wiki Atwiki アットウィキ



円周角




高校数学a 円周角と中心角のおさらい 例題編 映像授業のtry It トライイット




中3 数学 円に内接する四角形の問題です この問題がわからないので 教 数学 教えて Goo



円と三角形 角度 中学から数学だいすき




57 円に内接する三角形 と 円に内接する四角形 を比べる とちぎeライブラリ
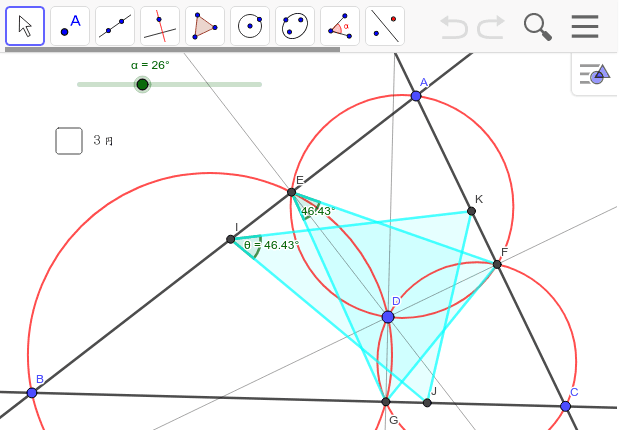



三角形に内接する相似三角形 Geogebra
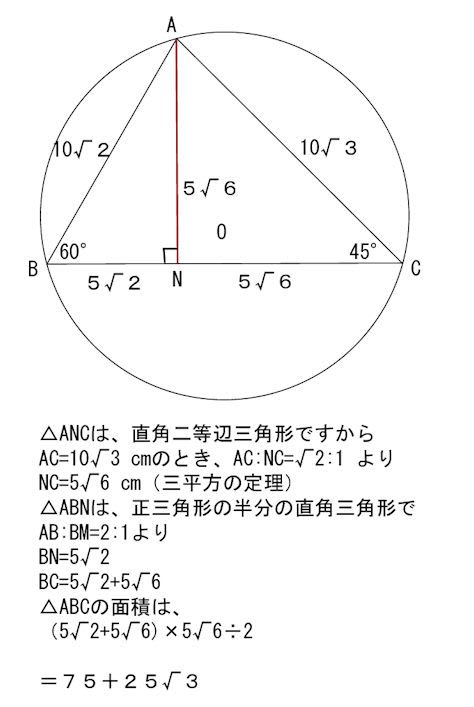



円に内接する 三角形の 問題 4 名寄 算数数学教室より
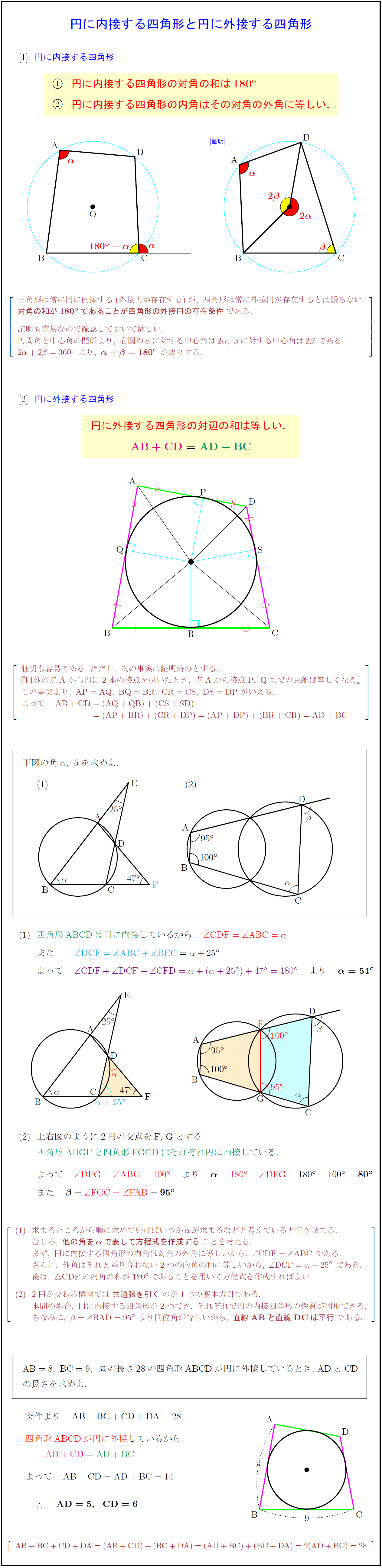



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月




円に内接する四角形の性質 高校数学の知識庫



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog



円に内接する二等辺三角形 駒場東邦中学 04年 パズル おもしろ算数問題



円に内接する四角形



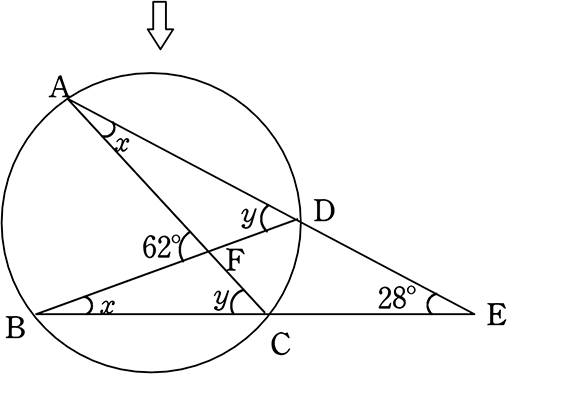
七五三 三角形から円に内接する四角形へ




この2つの問題の角xの部分の解き方と答えを教えてください Clear




Math 円 5 直角三角形に内接する円の半径 働きアリ




接線と円の関係 Jsciencer




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
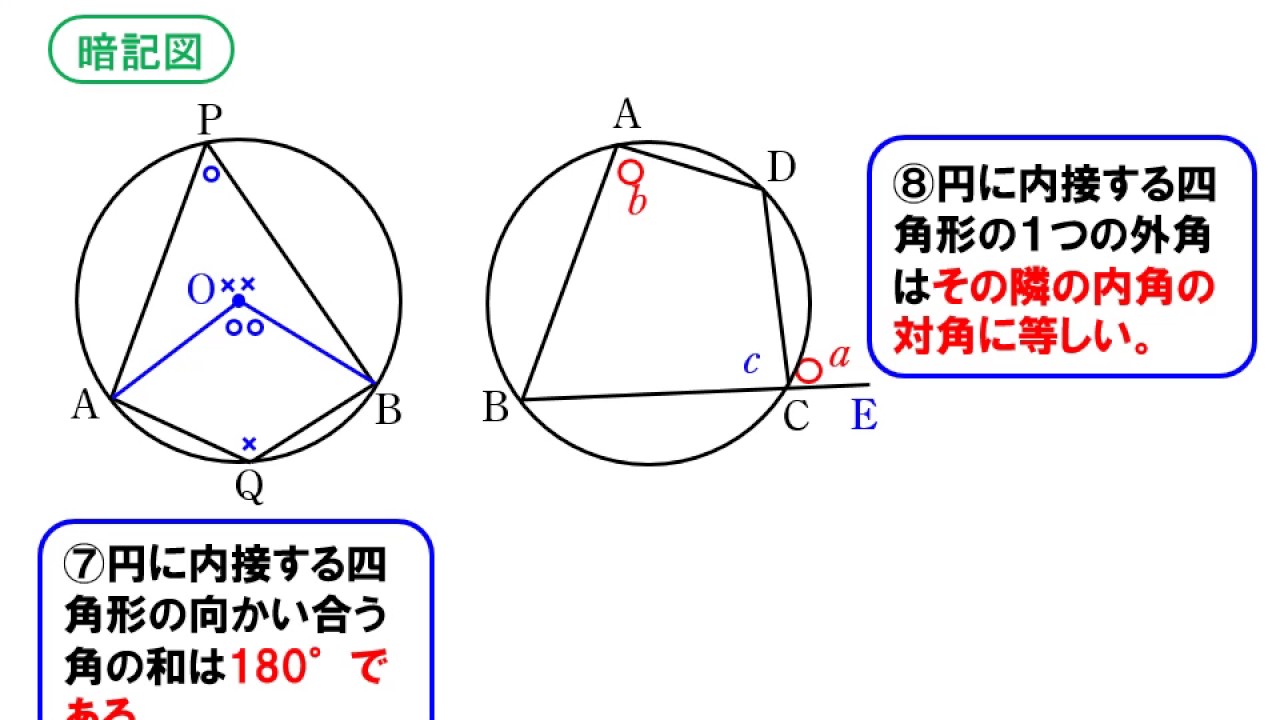



円と角度04 内接四角形の性質 Youtube
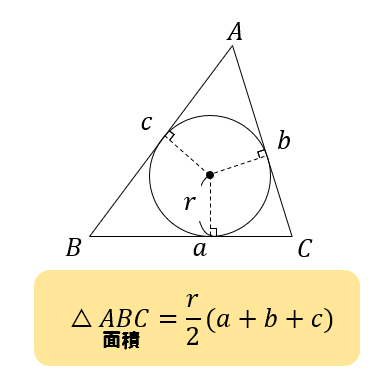



三角比 内接円の半径の求め方をイチから丁寧にやってみよう 数スタ



円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室



中学数学 円周角 中心角



円に内接する四角形 苦手な数学を簡単に



円周角の定理と中心角 中学3年数学 Youtube
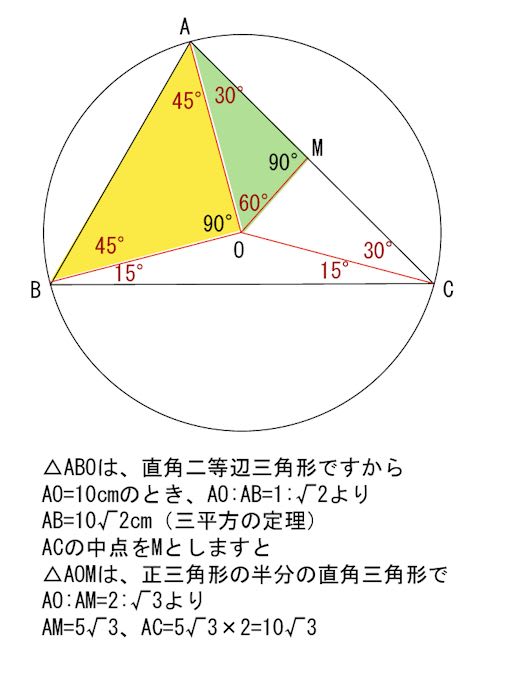



円に内接する 三角形の 問題 3 名寄 算数数学教室より
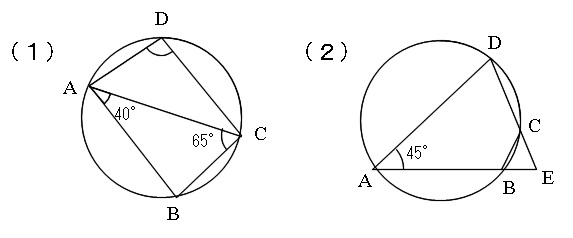



方べきの定理 公式 の覚え方と円に内接する四角形の対角線の性質
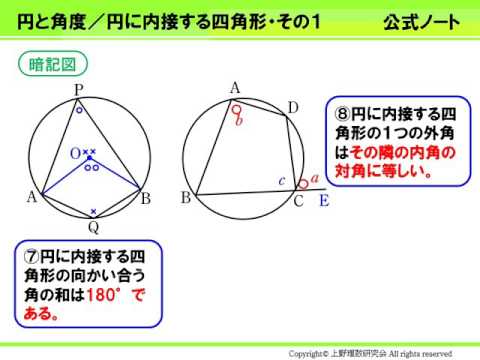



円と角度04 内接四角形の性質 Youtube




高校数学 円に内接する四角形の計量 基本と裏技のまとめ トレミーの定理 ブラーマグプタの公式他 受験の月




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者




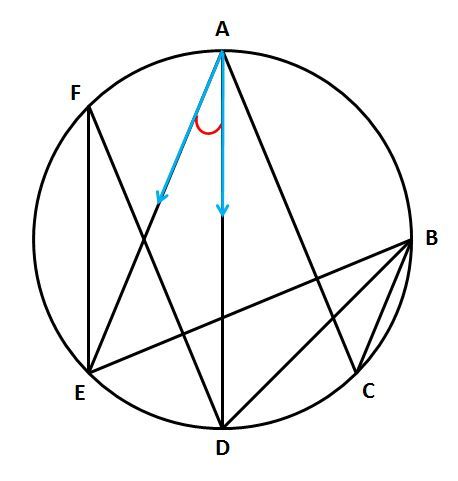
円に内接する三角形について 次の問題がわかりません 教えていただ 数学 教えて Goo



角度 円と四角形 中学から数学だいすき




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




中学数学 円周角 中心角




円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ
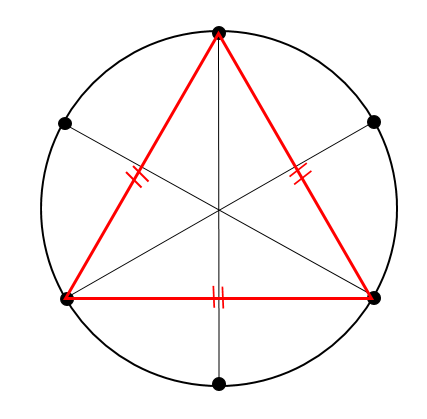



作図 円に内接する正三角形の作図方法とは 数スタ




高校数学 円に内接する四角形の対角線の長さと面積 受験の月



1




現代百姓のアタマん中 円周率の再考



七五三 三角形から円に内接する四角形へ




Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear
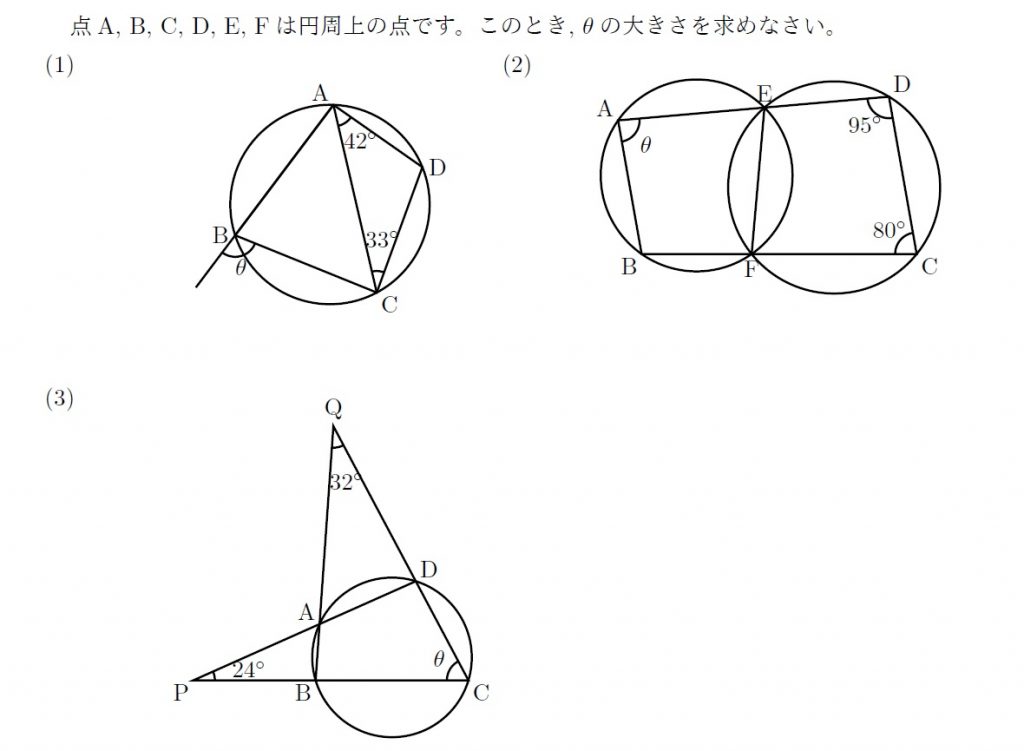



Emathソースコード 円に内接する四角形と角度 数樂管理人のブログ



七五三 三角形から円に内接する四角形へ



0 件のコメント:
コメントを投稿